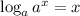Question

Show why the quotient property and power property are true.Quotient property:log_a(u)-log_a(v)=log_a(u/v)Power property:log_a(u)^n=nlog_a(u)Follow up questions:1. Explain why log_a1=0.2. Explain why log_a a^x=x is true if (if and only if) the base of the logarithm and the base used in the interior exponential function are identical.

Answer 1

We can show these statements by numerical instances:

Lets solve a numerical example of the power property.

`\log _a(u)^n=n\cdot\log _a(u)`

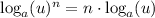
where a is the base of the logarithm.

If we choose a=3, u=9 and n=2, we have on the left hand side:

`\log _3(9)^2=\log _381=4`

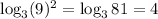
while on the right hand side, we obtain

`2\cdot\log _39=2\cdot2=4`

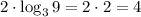
By comparing both results, we can see that the left hand side is equal to the right hand side, so the power propertuy is correct.

Lets take now the Quotient property:

`\log _a(u)-\log _a(v)=\log _a((u)/(v))`

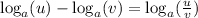
If we choose a=3, u =5 and v= 2, on the left hand side we have

`\begin{gathered} \log _3(5)-\log _3(2)=1.4649-0.6309 \\ \log _3(5)-\log _3(2)=0.834 \end{gathered}`

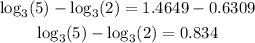
and on the right hand side of the property, we have

`\log _3((5)/(2))=\log _32.5=0.834`

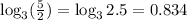
and we can see that both side coincide, then the property is correct.

1. Explain why log_a(1) =0.

We know that

`x^0=1`

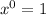
for any x.

If we apply logarithm on both sides, we have

`\log _ax^0=\log _a1`

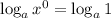
If we apply the power property on the left hand side, we have

`0\cdot\log _ax`

which is equal to zero. This means that

`0=\log _a1`

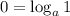
2. Explain why log_a a^x=x is true.

By means of the power property, we have

`\log _aa^x=x\cdot\log _aa`

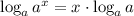
but

`\log _aa\text{ =1}`

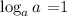
because the base (a) is the same as the number into the logarithm. Then, by substituting this result into the above equality, we have

`\log _aa^x=x\cdot\log _aa=x\cdot1=x`

then

`\log _aa^x=x`