We have the following points:
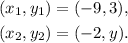
We must find the values of y such that the distance between the points is d = 8.
The distance between two points (x1, y1) and (x2, y2) is given by:
![d=\sqrt[]{(x_2-x_1)^2+\mleft(y_2-y_1\mright)^2}\text{.}](https://img.qammunity.org/2023/formulas/mathematics/college/ivhpt1dzfu2pp8gk4jf2p2ao8fnno5hjic.png)
Replacing the data of the problem in the equation above, we have:
![\begin{gathered} 8=\sqrt[]{(-2+9)^2+(y-3)^2}, \\ 8=\sqrt[]{49+(y-3)^2}\text{.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8znbxkwjf1iy9e3ccgueroa0n1acu9ktcm.png)
Solving the last equation for y, we get:
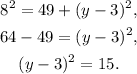
Taking the square root on both sides, we have:
![\begin{gathered} y-3=\pm\sqrt[]{15}, \\ y=3\pm\sqrt[]{15}\text{.} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9v74zyj3i5edjgl9moxrzi56hy07z54oin.png)
Rounding to one decimal place, we get:
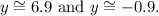
Rounding to two decimal places, we get:
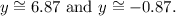
Answer
• Rounding to one decimal place: ,6,9,-0.9
,
• Rounding to two decimal places: ,6.87,-0.87