Question

The rate of inflation in the year 2014 was 2% per year. To get a sense of what this rate would mean in the long run, let's suppose that it persists through 2034.What would be the cost in 2034 of an item that costs $200 in 2014? (Round your answer to the nearest cent.)

Answer 1

Exponential Growth

Some natural events have a rate of growth that is proportional to the current amount of some given variable, like mass, money, population, etc.

Inflation gives an idea of how the value of something grows in time. Suppose the cost of an item is Co today. Its value grows at a certain rate r for a time t.

The future value of the item is:

`C(t)=C_o\cdot(1+r)^t`

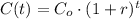
We know the cost of an item was Co=$200 in 2014. It grows at a constant rate of r=2% per year. Converting to decimal: r=0.02.

It's required to calculate the value of the item in the year 2034, that is, t=20 years from the initial year.

Substituting the data into the formula:

`C(20)=200\cdot(1+0.02)^(20)`

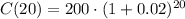
Calculating:

`\begin{gathered} C(20)=200\cdot(1.02)^(20) \\ C(20)=200\cdot(1.48595) \\ C(20)=297.19 \end{gathered}`

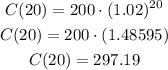
The cost of the item would be $297.19 in 2034