Answer:
f(x)=-0.3(x-2)²+5
• Option A: ,The vertex, (h,k) = (2, 5)
,
• Option E: ,Axis of Symmetry, x=2
• Option I: ,The focus is (2, 4 1/6)
f(x)=0.2(x+2)²-5
• Option C: ,The vertex, (h,k) = (-2, -5)
,
• Option F: ,Axis of Symmetry, x= -2
• Option G: ,The focus is (-2, 3 3/4)
Explanation:
Part A
Given the equation:
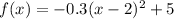
The standard equation of an up-facing parabola with a vertex at (h,k) and a focal length |p| is given as:
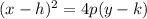
We rewrite the given equation in the form above:
![\begin{gathered} f(x)=-0.3(x-2)^2+5 \\ f(x)-5=-(3)/(10)(x-2)^2 \\ -(10)/(3)[f(x)-5]=(x-2)^2 \\ \left(x-2\right)^2=4(-(5)/(6))[f(x)-5] \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/h54soc0e2tvkmdwl1lf5sulop1ysxra8z7.png)
From the form above:
• Option A: ,The vertex, (h,k) = (2, 5)
,
• Option E: ,Axis of Symmetry, x=2
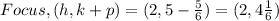
• Option I: ,The focus is (2, 4 1/6)
Part B
Given the equation:
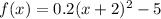
Rewrite the equation in the standard form given earlier:
![\begin{gathered} 0.2(x+2)^2=f(x)+5 \\ (x+2)^2=5[f(x)+5] \\ (x+2)^2=4((5)/(4))[f(x)+5] \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a22u4g5m75ozxl52y69b7dorlahnb184on.png)
From the form above:
• Option C: ,The vertex, (h,k) = (-2, -5)
,
• Option F: ,Axis of Symmetry, x= -2
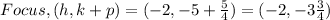
• Option G: ,The focus is (-2, 3 3/4)