It's important to know that a rectangle has opposite parallel equal sides, which means that the diagonal is a transversal between the parallels.
We can deduct that the angle 7y-2 and the angle 4y+13 are alternate interior angles because they are between parallels and at different sides of the transversal, which means those angles are equivalent.
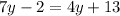
Let's solve for y, first, we subtract 4y from each side.
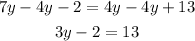
Then, add 2 on each side.
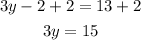
At last, divide both sides by 3.
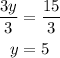
Once we have the value of y, we use it to find x. We know that the angle 5x+7 and the angle 7y-2 are complementary because if the figure is a rectangle, then all its interior angles measure 90°.
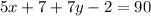
Now we use the value of y and solve for x.
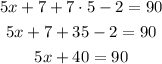
Subtract 40 from each side.
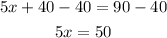
Divide both sides by 5.
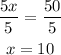
Therefore, the value of x is 10 and the value of y is 5.