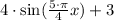Question

Write a sine function that has a midline of 3, an amplitude of 4 and a period of 8/5f(x)=

Answer 1

Recall that the general shape of a sine function is of the form

`A\sin (Bx-C)+D`

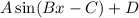
where A is the amplitude of the function, D is the midline, the number C/B is the phase shift and the number is 2*pi/B is the period of the function.

In our case, we are told that A=4 and D=3. Since we are told a value of the period, but nothing about the phase shift, we will assume that the phase shift is 0. Then, we have the following equations

`(C)/(B)=0`

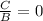
and

`(2\cdot\pi)/(B)=(8)/(5)`

Form the first equation, we can determine that C=0.

From the last equation, we can multiply both sides by 5*B, so we get

`8\cdot B=5\cdot2\cdot\pi=10\cdot\pi`

Finally, we divide both sides by 8, so we get

`B=(10\cdot\pi)/(8)=(5\cdot\pi)/(4)`

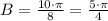
So, we end up with the following formula

`4\cdot\sin ((5\cdot\pi)/(4)x)+3`