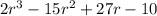Question

Is (r-5) a factor of 2r^3-15r^2+27r-10?

Answer 1

To answer this question, we have to remember that:

Then, if (r - 5) is a factor of the given polynomial, if we substitute r by 5, that is, r = 5, into the polynomial, and if the result is zero, then the factor (x - 5) is a factor of the polynomial.

Then we have that:

`f(r)=2r^3-15r^2+27r-10`

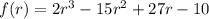
Now, we have to evaluate the polynomial for x = 5:

`\begin{gathered} f(5)=2(5)^3-15(5)^2+27(5)-10 \\ f(5)=2(125)-15(25)+135-10 \\ f(5)=250-375+135-10 \\ f(5)=-375+(250+135-10) \\ f(5)=-375+375=0 \\ f(5)=0 \end{gathered}`

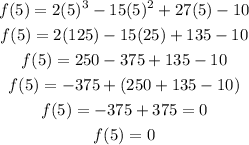
Since r = 5 is a root of the equation f(r) = 0, then (r - 5) is a factor of f(r).

In summary, (r - 5) is a factor of the given polynomial:

`2r^3-15r^2+27r-10`