Question

The gravitational force, Fbetween an object and the Earth is inversely proportional to the square of the distance from the object to the center of the Earth. If an astronaut weighs 214 pounds on the surface of the Earth, what will this astronaut weigh 500 miles above the Earth? Assume that the radius of the Earth is 4000m / l * es Round off your answer to the nearest pound)

Answer 1

169 pounds

Explanation:

We can calculate the weight of the astronaut since we know the relationship between both variables (weight and radius), so we establish the following proportion:

`(W_2)/(W_1)=(R^2)/((R+d)^2)`

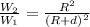
The astronaut's initial weight is 214 pounds (W1), the radius is 4000 miles (R) and the distance is equal to 500 miles, we substitute and calculate the new weight of the astronaut as follows:

`\begin{gathered} W_2=W_1\cdot(R^(2))/((R+d)^(2)) \\ \\ \text{ We replacing} \\ \\ W_2=214\cdot(4000^2)/(\left(4000+500\right)^2) \\ \\ W_2=169.086=169\text{ pounds} \end{gathered}`

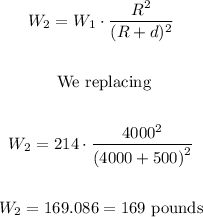
The astronaut's new weight is 169 pounds