Question

Write a system of equations to describe the situation below, solve using substitution, and fillin the blanks.Charlie plans to attend the Jefferson County Fair and is trying to decide what would be abetter deal. He can pay $39 for unlimited rides, or he can pay $15 for admission plus $1 perride. If Charlie goes on a certain number of rides, the two options wind up costing him thesame amount. How many rides is that? What is that cost?If Charlie ger on

Answer 1

Given:

In the first option, Charlie can pay $39 for unlimited rides,

In the second option, Charlie can pay $15 for admission plus $1 per ride.

Required:

We need to find the number of rides that the two options wind up costing him the same amount.

Step-by-step explanation:

Let C be the cost of the ride.

Let r be the number of the ride.

Consider the first option.

`C=39`

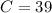
Consider the second option.

`C=15+r(1)`

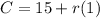
Substitute C=39 in this equaiton.

`39=15+r(1)`

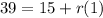
Substract 15 from both sides of the equation.

`39-15=15+r(1)-15`

`24=r`
`r=24\text{ rides.}`

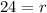
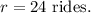
The number of rides that the two options wind up costing him the same amount is 24 rides.

The cost of the ride is C =39.

Final answer:

The number of rides =24.

The cost of the rides =39.