Question

(3) The volume of a fixed mass of gas is V. If the pressure of the gas isdoubled and its absolute temperature is reduced to half of the initial value,the volume of the gas becomes

Answer 1

the volume of the gas becomes 1/4 the original volume

Step-by-step explanation:

The ideal gas law gives the following relationship between temperature, pressure, and volume:

`PV=n\cdot r\cdot T`

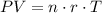
where

P = pressure

V = volume

n = number of moles

r = gas constant

T = temperature

Now let us call the initial pressure, volume, and temperature P0, V0, and T0 respectively; then we have

`P_0V_0=\text{nrT}_0`

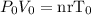
Solving for V0 gives

`\boxed{V_0=\frac{\text{nrT}_0}{P_0}}`

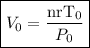
Now, what happens if the new pressure is 2 times the initial pressure ( P = 2 P0) and the new temperature is reduced to half ( T = 1/2 T0).

We find out by putting in P = 2 P0 and T = 1/2 T0 into the above equation to get:

`V=\frac{nr((1)/(2)T_0)_{}}{2P_0}`

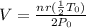
which simplifies to give us

`V=\frac{nrT_0_{}}{4P_0}=(1)/(4)((nrT_0)/(P_0))`

Realising that

`V_0=\frac{\text{nrT}_0}{P_0}`

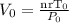
the above becomes

`V=(1)/(4)((nrT_0)/(P_0))=(1)/(4)V_0`

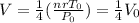
Hence, our final result is

`\boxed{V=(1)/(4)V_0}`

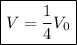
meaning that the new volume is one-fourth of the original volume.