Question

The equation for line A is y=1/3x+4 suppose line A is parallel to line B and point (-3,1) lies on line B select the equation which represents line B in slope intercept form

Answer 1

As given by the question

There are given that the equation of line A is:

`y=(1)/(3)x+4`

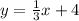
Now,

From the given equation, the value of slope is:

`m=(1)/(3)`

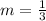
Parallel lines have equal slope, thus

`y=(1)/(3)x+c`

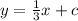
The above equation is the line B.

So,

To find the c, substitute the given point (-3, 1) into the partial equation of B

Then,

`\begin{gathered} y=(1)/(3)x+c \\ 1=(1)/(3)*(-3)+c \\ 1=-1+c \\ c=2 \end{gathered}`

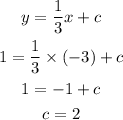
Then

Put the value of c into the above equation

`\begin{gathered} y=(1)/(3)x+c \\ y=(1)/(3)x+2 \end{gathered}`

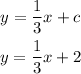
So, the above equation is the equation of line B.

Hence, option D is correct.