A reflection over the line y=x implies exchanging the x and y coordinates of a point. For example if you take a generic point (a,b) then its reflection over y=x is (b,a). Our point is (-1,3) so its reflection over y=x is the point (3,-1).
Then we have to translate it two units left. Translating a point left means that we are moving towards negative x values so we need to substract 2 from the x coordinate:
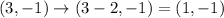
Finally we have to translate it 1 unit up towards positive y values so we have to add 1 to its y coordinate:
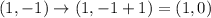
And these are the final coordinates. In the following picture you have the points you get after each step (from A to D) with the y=x line in blue: