The zeros of the polynomial are: -5, 3 and i.
The zeros are the x-values that make each factor equal to zero, then if -5 is a zero:
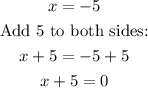
then (x+5) is one of the factors.
Zero: 3, thus:
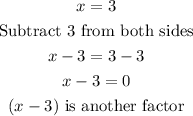
Zero: i, thus:
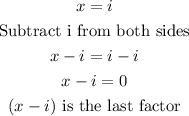
A possible factorization of the polynomial is: (x+5)(x-3)(x-i)