Question

f(x) = x2. What is g(x)?SIf(x)= x/g(x)(2,1)-5O A.06)-()O B. g(x) = 2x2O C. g(x)-9(x)=(*)O D. g(x)= x2

Answer 1

Step-by-step explanation

As you can see all the possible answers have the same form:

`g(x)=ax^2`

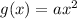
By looking at the picture you'll notice that the graph of g(x) has to pass through the point (2,1). Remember that the points in the graph of g(x) have the form (x,g(x)). Since (2,1) is part of the graph of g(x) then we have the following:

`\begin{gathered} (2,1)=(x,g(x)) \\ x=2 \\ g(2)=1 \end{gathered}`

So let's evaluate the expression for g(x) that we wrote before at x=2. This way we'll obtain an equation for the number a:

`\begin{gathered} g(2)=1=a\cdot2^2 \\ 1=4a \end{gathered}`

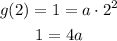
Then we can divide both sides by 4:

`\begin{gathered} (1)/(4)=(4a)/(4) \\ a=(1)/(4) \end{gathered}`

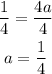
Then we get:

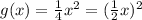
`g(x)=(1)/(4)x^2=((1)/(2)x)^2`Answer

Then the answer is option A.