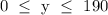SOLUTION:
Step 1:
We are to find an appropriate expresson for the range for the number of Chirps.
Step 2;
The equation given is y = 5x - 30
The range of x given;
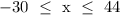
Step 3:
We substitute both the lowest and greatest value into the equations;
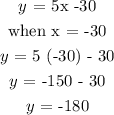
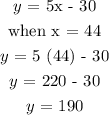
Step 4:
It is very obvious that the number of Chirps can never be negative so we need to ignore the -180 and set our range to start from zero.
We now have;