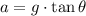Question

A student uses a plumb bob to verify that the doorjamb in a car is vertical. As the car pulls away from a stop, the studentobserves that the string now makes an angle 8 with the doorjamb. What is the acceleration of the car?Select one:O a. g tan iO b. gì,O c. g sin iO d. I.O e. gcos i,

Answer 1

There are two forces acting on the plumb bob: the force of gravity (weight) and the tension of the string. According to Newton's Second Law of Motion, the sum of these two forces must be equal to the mass of the plumb bob times its acceleration:

`\begin{gathered} \Sigma\vec{F}=m\vec{a} \\ \Rightarrow\vec{T}+\vec{W}=m\vec{a} \end{gathered}`

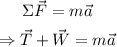
Draw a diagram to identify the components of each force:

Observe that the vertical component of the tension is equal to T*cos(θ), and it must balance the weight of the mass. On the other hand, the horizontal component of the tension is T*sin(θ) and it is responsible for the acceleration of the mass. Then:

`\begin{gathered} T\cos \theta-W=0 \\ \Rightarrow T=(W)/(\cos \theta) \end{gathered}`

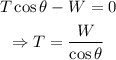
Since W=mg, then:

`T=(mg)/(\cos \theta)`

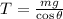
On the other hand:

`\begin{gathered} T\sin \theta=ma \\ \Rightarrow(mg)/(\cos\theta)\sin \theta=ma \\ \Rightarrow(\sin \theta)/(\cos \theta)g=a \\ \Rightarrow a=g\cdot\tan \theta \end{gathered}`

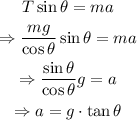
Therefore, the acceleration of the car is given by the expression is:

`a=g\cdot\tan \theta`