SOLUTION
The formula for finding the confidence interval is:
![CI=\bar{x}\pm Z^{}(\frac{\sigma}{\sqrt[]{n}})](https://img.qammunity.org/2023/formulas/mathematics/college/ox3ulxp3bblhg6ypqqkdhvo42kwo9133qo.png)
mean=21.3
S.D=2.3
Sample size (n) =150
From theory, the critical value (Z) for a 99% confidence interval is 2.58
So Z=2.58
Substituting all these parameters into the confidence interval formula,
we will obtain:
![CI=21.3\pm(2.58*(\frac{2.3}{\sqrt[]{150}}))](https://img.qammunity.org/2023/formulas/mathematics/college/b5or4itcla53sxo3hydbp0d8yypfa5gjc7.png)
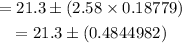

The final answer is 21.78 to 20.82 confidence interval.