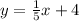Question

Write the slope-intercept form of the equation of each line?

Answer 1

Problem 1

It appears the line is going through the points (-1,-4) and (0,5)

Let's find the slope

`(x_1,y_1) = (-1,-4) \text{ and } (x_2,y_2) = (0,5)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (5 - (-4))/(0 - (-1))\\\\m = (5 + 4)/(0 + 1)\\\\m = (9)/(1)\\\\m = 9\\\\`

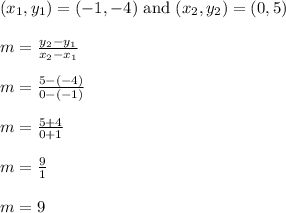
The slope is 9

The y intercept is b = 5 as this is where the graph crosses the y axis.

We go from y = mx+b to y = 9x+5

Answer: y = 9x+5

=======================================================

Problem 2

This line goes through the points (0,4) and (5,5)

We'll follow the same exact steps as before

First we need the slope

`(x_1,y_1) = (0,4) \text{ and } (x_2,y_2) = (5,5)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (5 - 4)/(5 - 0)\\\\m = (1)/(5)\\\\`

The y intercept is the y coordinate of (0,4) so it's b = 4

Answer:
`y = (1)/(5)x+4`