A function is a relation in which each input has only one output. When we consider a set of ordered pairs, a function does not have two similar values for x. That is for example, {(2,1) , (2,3)} is not a function where as, {(1,3), (2,3)} is a function.
Therefore from the given sets,
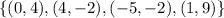
is a function.