Question

Consider the following data: 3, 9, 4, 4, 4, 9, 9 Calculate the value of the sample variance. Round your answer to one decimal place.

Answer 1

8

Step-by-step explanation:

To find the value of the sample variance, we use the formula below:

`\text{Var}=\frac{\sum ^{}_{}(x_i-\bar{x})^2}{n-1}`

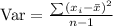
First, we determine the mean of the data: 3, 9, 4, 4, 4, 9, 9

`\begin{gathered} \text{Mean}=(3+9+4+4+4+9+9)/(7) \\ =(42)/(7) \\ \bar{x}=6 \end{gathered}`

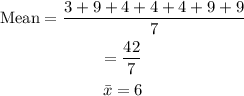
Next, we find the sum of the squares of the mean deviation.

`\begin{gathered} \sum ^{}_{}(x_i-\bar{x})^2=(3-6)^2+(9-6)^2+(4-6)^2+(4-6)^2+(4-6)^2+(9-6)^2+(9-6)^2 \\ =(-3)^2+(3)^2+(-2)^2+(-2)^2+(-2)^2+(3)^2+(3)^2 \\ =9+9+4+4+4+9+9 \\ \sum ^{}_{}(x_i-\bar{x})^2=48 \end{gathered}`

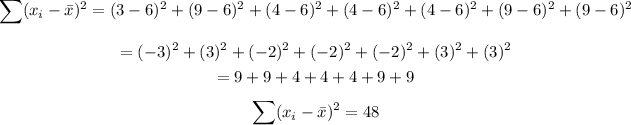
Therefore, the sample variance is:

`\begin{gathered} \text{Var}=\frac{\sum^{}_{}(x_i-\bar{x})^2}{n-1}=(48)/(7-1) \\ =(48)/(6) \\ =8 \end{gathered}`

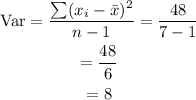
The sample variance is 8.