Solution
Question 1.
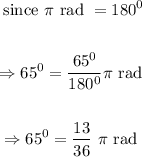
Question 2.
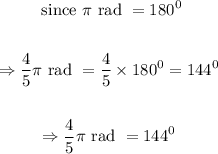
Question 3.
Idea: The reference angle is the smallest possible angle made by the terminal side of the given angle with the x-axis
For second quadrant, the corresponding angle is 180 - x => 180 - 81 = 99
For third quadrant, the corresponding angle is 180 + x => 180 + 81 = 261
For fourth quadrant, corresponding angle is 360 - x => 360 - 81 = 279
Hence, the other 3 parameters are, 99, 261, and 279
Question 4.
since 320 falls in the fourth quadrant, its reference angle is just 360 - 320 = 40
Therefore, its reference angle is 40 degrees.