Question

What is the probability of drawing each of the following cards from a standard playing deck? See the entry "playing cards" in the glossary tolearn what playing cards are included in a deck.» Hint:a. P(Jack)b. P(spade)c. P(Jack of spades)d. P(not spade)

Answer 1

In a deck of 52 cards we have:

4 aces

4 kings

4 queens

4 jacks

36 number cards

We can calculate the probability as the quotient between the positive outcomes (when we draw the card we are looking for) divided by the total possible outcomes (in this case, the total number of cards).

a. P(Jack)

There are 4 jacks in the 52 cards, so the probability is:

`P=(x)/(N)=(4)/(52)\approx0.077`

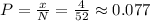
b. P(spade)

One fourth of the deck of cards is spades, so the probability is 1/4=0.25

c. P(Jack of spades)

There is only one jack of spades in the deck of cards, so the probability of drawing a jack of spades is 1/52=0.019

d. P(not spade)

We know that the probability of drawing a spade card is 1/4, so the probability of not drawing a spade card is (1-1/4)=3/4=0.75.

We can also calculate as the number of cards that are not spades (3*13=39) divided by the total amount of cards (52),

Then we have P(not spade) = 39/52 = 0.75