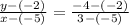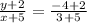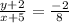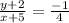To solve this problem, we need to apply the formula for the equation of a straight line.
One of the forms of this formula, which is appropriate for this problem, is as follows:
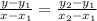
Where (x1 , y1) and (x2 , y2), are the coordinates of any two points that lie on the line.
In this case, the coordinates are: ( -5,-2), and (3, -4)
Now: