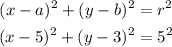Question

Write an equation (in standard form) for a circle with endpoints of its diameter located at (2, -1) and (8, 7).

Answer 1

Step 1 :

In this question, we are given that the circle has endpoints of its diameter located at (2, -1 ) and (8, 7).​

Next, we meant to find the mid-point of the two [points , which we will take the centre :

`\begin{gathered} (a,b)=(\frac{x_{1\text{ + }}x_2}{2},(y_1+y_2)/(2))_{} \\ (x_1,y_1\text{ ) = ( 2 , - 1 )} \\ (x_2,y_2\text{ ) = ( 8, 7 )} \end{gathered}`
`\begin{gathered} (\text{ a , b ) = ( }\frac{2\text{ + 8}}{2}\text{ , }\frac{-1\text{ + 7}}{2}) \\ =\text{ ( }(10)/(2)\text{ , }(6)/(2)) \\ (a,b)=\text{ ( 5, 3 )} \end{gathered}`

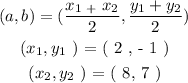
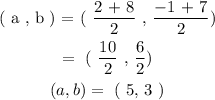
Step 2 :

Next, we need to distance between the centre and one of the end-points.

We need to find the distance of ( 2, - 1) and ( 5, 3 ) which we are to take as the radius.

We use the formula:

`\begin{gathered} r\text{= }\sqrt[]{(x_2\text{ - }}x_1)^2+(y_2-y_{1\text{ }})^2 \\ r\text{ = }\sqrt[]{(5-2)^2+(3--1)^2} \\ r\text{ = }\sqrt[]{3^2+4^2} \\ r\text{ = }\sqrt[]{9+\text{ 16}} \\ r\text{ = }\sqrt[]{25} \\ r\text{ = 5} \end{gathered}`

Step 3 :

We can see clearly that the centre( a , b ) = ( 5, 3 ) and radius 5

Then, we have that the equation of the circle ( in standard form ) is given as :

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ (x-5)^2+(y-3)^2=5^2 \end{gathered}`