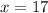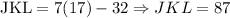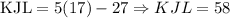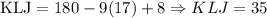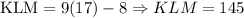Question

Solve for X, then find the measure of each angle.X=JKL=KJL=KLJ=KLM=

Answer 1

We will have the following:

7x - 32 & 5x -27 & 180 -(9x -8)

The last onse since we are given the exterior angle that is supplementary from the angle we need, we then proceed as follows:

`(7x-32)+(5x-27)+(180-9x+8)=180`

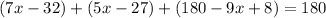
That since the sum of all internal angles of a triangle equals 180°, we now solve for x:

`\Rightarrow3x+129=180\Rightarrow3x=51\Rightarrow x=17`

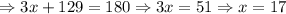
Now that we have x, we then replace in the functions, and we will get:

`x=17`
`\text{JKL}=7(17)-32\Rightarrow JKL=87`
`\text{KJL}=5(17)-27\Rightarrow KJL=58`
`\text{KLJ}=180-9(17)+8\Rightarrow KLJ=35`
`\text{KLM}=9(17)-8\Rightarrow KLM=145`