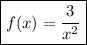Reciprocal Power Function
The graph shows two branches that have a vertical asymptote at x = 0.
To find the domain of the function, we use the vertical line method that consists of moving an imaginary vertical line throughout the x-axis. If the line touches the graph at a certain value of x, then that value is part of the domain.
It's clear that any value of x is part of the domain except x = 0 because it's a vertical asymptote, thus:
Domain= (-∞, 0) U (0, +∞)
The range can be found in a similar way but using a horizontal line. The line touches the function at every value of y that is positive, thus the range is.
Range. (0, +∞)
The function can be represented by the expression:
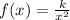
Where k is a constant that can be determined by using one of the given points, for example, (1, 3). Substituting:
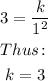
The reciprocal power function is: