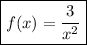Question

Given the following graph. State the domain and range. Provide the reciprocal power function represented by this graph

Answer 1

Reciprocal Power Function

The graph shows two branches that have a vertical asymptote at x = 0.

To find the domain of the function, we use the vertical line method that consists of moving an imaginary vertical line throughout the x-axis. If the line touches the graph at a certain value of x, then that value is part of the domain.

It's clear that any value of x is part of the domain except x = 0 because it's a vertical asymptote, thus:

Domain= (-∞, 0) U (0, +∞)

The range can be found in a similar way but using a horizontal line. The line touches the function at every value of y that is positive, thus the range is.

Range. (0, +∞)

The function can be represented by the expression:

`f(x)=(k)/(x^2)`

Where k is a constant that can be determined by using one of the given points, for example, (1, 3). Substituting:

`\begin{gathered} 3=(k)/(1^2) \\ Thus\colon \\ k=3 \end{gathered}`

The reciprocal power function is:

`\boxed{f(x)=(3)/(x^2)}`