We must find the volume of a box with:
• square base with diagonal ,h = 6 cm,,
,
• height ,H = 15 cm,.
1) First we compute the length of the sides of the square base.
From the diagram above, we see that the diagonal of the box constitutes the hypotenuse of a triangle of sides a. Pitagoras Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other sides, so we have:
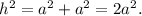
Replacing the value h = 6 cm, and solving for a², we get:
![\begin{gathered} (6\operatorname{cm})^2=2a^2, \\ 36cm^2=2a^2, \\ a^2=(36cm^2)/(2), \\ a^2=18cm^2\text{.} \end{gathered}]()
2) The volume is given by the product of height (H) and the area of the base (a²):
![V=H\cdot a^2=15\operatorname{cm}\cdot18cm^2=270cm^3.]()
Answer
The volume of the box is 270 cm³.