Question

Hannah has to make 261 gallons of punch for a big party. The punch is made of soda and fruit drink. The cost of the soda is $1.73 per gallon and the cost of the fruit drink is $2.60 per gallon. Hannah's budget requires that the punch cost $2.36 per gallon. How many gallons of soda and how many gallons of fruit drink does she need?

Answer 1

We have to find how many gallons of soda and how many gallons of fruit drink she needs for the 261 gallons of punch to cost $2.36 per gallon.

We know that a gallon of soda (S) costs $1.73 and a gallon of fruit drink (F) costs $2.60.

We can write two equations to find the value of S, the number of gallons of soda, and F, the number of gallons of fruit drink.

We know that the total number of gallons, the sum of S and F, is 261 gallons. We can express it as an equation as:

`S+F=261`

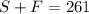
The sum of the cost of the soda, expressed as the price per gallon times the number of gallons: 1.73*S, and the cost of the fruit drink, 2.60*F has to be equal to the total cost of the punch.

The cost of the punch is equal to the cost per gallon, $2.36, and the number of gallons, 261 gal.

We can express this as an equation as:

`\begin{gathered} 1.73\cdot S+2.60\cdot F=2.36\cdot261 \\ 1.73S+2.60F=615.96 \end{gathered}`

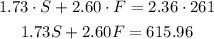
Now, we have a system of equations:

`\begin{cases}S+F=261 \\ 1.73S+2.60F=615.96\end{cases}`

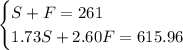
We can express S in function of F using the first equation and then replace it in the second equation:

`\begin{gathered} S+F=261 \\ S=261-F \end{gathered}`
`\begin{gathered} 1.73S+2.60F=615.96 \\ 1.73(261-F)+2.60F=615.96 \\ 451.53-1.73F+2.60F=615.96 \\ 451.53+0.87F=615.96 \\ 0.87F=615.96-451.53 \\ 0.87F=164.43 \\ F=(164.43)/(0.87) \\ F=189 \end{gathered}`

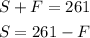
We can use the first equation now to find the value of S:

`\begin{gathered} S=261-F \\ S=261-189 \\ S=72 \end{gathered}`

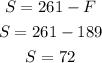
Answer:

The number of gallons of soda is 72 gallons.

The number of gallons of fruit drink is 189 gallons.