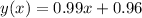Let:
x = duration of each call
y = cost of the call
Since the cost of the call and the length of the call are related. we can model the situation as a linear equation of the form:

a 5-minute overseas call costs $5.91 and a 10-minute call costs $10.86, so:

Let:

Using elimination method:
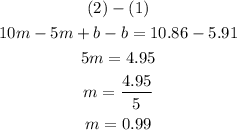
Replace the value of m into (1):
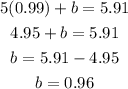
Therefore, the cost as a function of time is: