Solution:
Given:
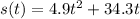
where;
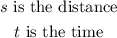
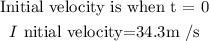
To get the time the stone will hit the ground from a height of 480.2m,

Solving the quadratic equation to get the value of t,
![\begin{gathered} \text{Multiplying the equation all through by 10,} \\ 4.9t^2+34.3t-480.2=0\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots X10 \\ 49t^2+343t-4802=0 \\ \\ U\sin g\text{ quadratic formula;} \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a} \\ \\ \text{where,} \\ 49t^2+343t-4802=0 \\ a=49 \\ b=343 \\ c=-4802 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vjyj0lxqfh11egm180btgsb1iws8lros8y.png)
Substituting these values into the quadratic formula,
![\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}_{}}{2a} \\ t=\frac{-343\pm\sqrt[]{343^2-(4*49*-4802)}}{2(49)} \\ t=\frac{-343\pm\sqrt[]{117649-(-941192)}}{98} \\ t=\frac{-343\pm\sqrt[]{117649+941192}}{98} \\ t=\frac{-343\pm\sqrt[]{1058841}}{98} \\ t=(-343\pm1029)/(98) \\ t_1=(-343+1029)/(98)=(686)/(98)=7 \\ t_2=(-343-1029)/(98)=(-1372)/(98)=-14 \\ \\ \text{Hence, the time is } \\ t=7,t=-14 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/4vm39wlr990idxv9815qalxpw62lyzwisx.png)
Since time can not be negative, we discard t = -14 and go with the positive value of time.
Therefore, the time it will take the stone to hit the ground is 7 seconds.
Hence, it will take 7seconds to hit the ground.