Solution:
The coordinate given is
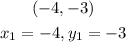
The slope given is

The general equation of a line is given below as

Concept:
The formula to calculate the equation of a line when one slope and one point is given is
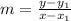
Step 1:
Substitute the values in the formula above

Step 2:
Cross multiply the equation above
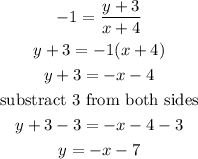
Hence,
The equation of the line is y = -x -7
where the slope is m = -1
the y-intercept is b = -7