Question

For the Function f(x) x ^3 cm on the interval [1,5]

Answer 1

1) Divide [1,5] into four subintervals of equal length, as shown below

`\lbrack1,5\rbrack=\lbrack1,2\rbrack\cup\lbrack2,3\rbrack\cup\lbrack3,4\rbrack\cup\lbrack4,5\rbrack`

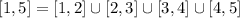
The left endpoints of each interval are

`u_1=1,u_2=2,u_3=3,u_4=4`

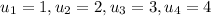
Thus, the approximate area A is

`\begin{gathered} \Rightarrow A=f(u_1)(2-1)+f(u_2)(3-2)+f(u_3)(4-3)+f(u_4)(5-4) \\ \Rightarrow A=f(u_1)+f(u_2)+f(u_3)+f(u_4) \\ \Rightarrow A=1^3+2^3+3^3+4^3=100 \end{gathered}`

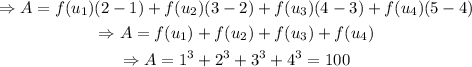
The approximate area in part 1) is A=100

2) Similarly, divide [1,5] into 8 subintervals,

`\lbrack1,5\rbrack=\lbrack1,1.5\rbrack\cup\lbrack1.5,2\rbrack\cup...\cup\lbrack4,4.5\rbrack\cup\lbrack4.5,5\rbrack\rightarrow\text{ length of interval equal to 0.5}`

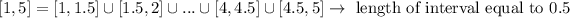
And

`u_1=1,u_2=1.5,...,u_7=4,u_8=4.5`

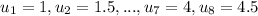
Thus,

`\begin{gathered} \Rightarrow A=0.5(f(u_1)+f(u_2)+...+f(u_7)+f(u_8)) \\ \Rightarrow A=0.5(1^3+1.5^3+...+4^3+4.5^3) \\ \Rightarrow A=0.5(253) \\ \Rightarrow A=126.5 \end{gathered}`

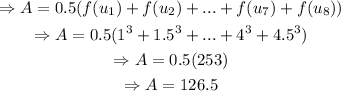
The approximate area in part 2) is 126.5.

3) The area under the curve is given by an integral of f(x) on the interval; thus,

`A=\int_1^5x^3dx=156`

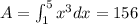
4)