To solve the expression:
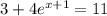
The first step is to leave the exponential term alone on the left side of the equation:
-Pass 3 to the right side by applying the opposite operation to both sides of it:
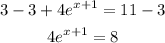
-Divide both sides by 4
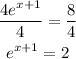
-To take the x-term from the exponent place, apply the natural logarithm to both sides of the expression
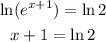
-Finally, pass 1 to the right sides of the expression by applying the opposite operation to both sides of the equal sign:
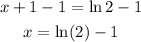
The correct option is the first one.