Question

Foe eaxh Arithmetic sequence, identify the next 3 terms of the sequence 11, 111,......

Answer 1

The nth term of an Arithmetic sequence is found as follows:

`a_n=a_1+(n\text{ - 1)d}`

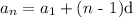
where a1 is the first term, and d is the common difference. In this case:

a1 = 11

d = 111 - 11 = 100

Then, the third, fourth and fifth terms of the sequence are:

`\begin{gathered} a_3=11+(3\text{ - 1)100 = 211} \\ a_4=11+(4\text{ - 1)100 = 311} \\ a_5=11+(5\text{ - 1)100 = 411} \end{gathered}`

The sequence is 11, 111, 211, 311, 411