There are two ways to calculate the accrued amount, assuming that the account pays simple interest.
1)
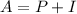
2)
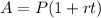
Where
A is the accrued amount
P is the principal amount
I is the interest amount
r is the interest rate expressed as a decimal value
t is the time expressed in years
Using both equations you can calculate the accrued amount and the principal amount.
What you have to do is equal both expressions:
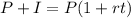
Now we have determined an expression with P as it's only unknown since we know the interest (I), the interest rate (r), and the time period (t)
To determine P, first, you have to express the interest rate as a decimal value and the time period in years.
Interest rate: R=2%, divide the percentage by 100:
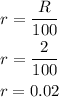
Time period: t=180 days, to express this value in years, you have to divide it by the number of days in one year. Assuming that there are 365 days in one year, the calculation is the following:
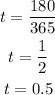
Using I=350, r=0.02, and t=0.5 you can calculate P:
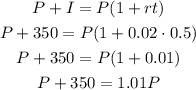
Subtract P to both sides of the equal sign to pass the term to the right:
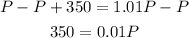
Divide both sides by 0.01
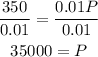
The principal amount is P= $35,000
Add the interest and the principal amount to determine the accrued amount:
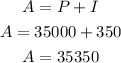
The accrued amount is A= $35,350