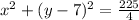Question

Write the equation in standard form for the circle with center (0,7) passing through (6,5/2

Answer 1

The equation in standard form for the circle is given by:

`(x-a)^2+(y-b)^2=r^2`

where the center is (a, b) and the radius is r.

Then, we can replace the point (6, 5/2) and the center (0, 7) in the equation to find r:

`(6-0)^2+((5)/(2)-7)^2=r^2`

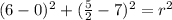
Simplifying the expressions inside the parenthesis:

`(6)^2+((5-7*2)/(2))^2=r^2`
`36+((5-14)/(2))^2=r^2`
`36+((-9)/(2))^2=r^2`
`36+(81)/(4)=r^2`
`(225)/(4)=r^2`

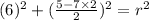
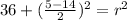
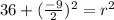
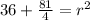
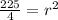
Then:

`r^2=(225)/(4)`

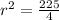
Finally, the equation is:

`(x-0)^2+(y-7)^2=(225)/(4)`

Answer:

`x^2+(y-7)^2=(225)/(4)`