Question

A basketball team sells tickets that cost $10, $20, or for VIP seats. $30. The team has sold 3138 tickets overall It has sold 160 more $20 tickets than $10 tickets. The total sales are $59.060. How manytickets of each kind have been sold?How many $10 tickets were sold?Help me solve thisView an exampleGet more helpClear

Answer 1

The regular tickets cost 1: $10

The regular tickets cost 2: $20

VIP setas cost: $30

The total number of sold tickets is 3138

They sold 160 more $20 tickets than $10 tickets

Total sales are $59,060.

To find how many $10 tickets have been sold, let's make a system of equations:

First equation:

`x+y+z=3138\text{ Eq. (1)}`

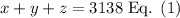
Where x is the number of $10 tickets sold, y is the number of $20 tickets sold, and z is the number of $30 tickets sold.

Second equation:

`y=x+160\text{ Eq.(2)}`

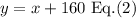
And third equation:

`10x+20y+30z=59060`

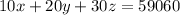
Start by replacing Eq. (2) into the other two equations:

`\begin{gathered} x+(x+160)+z=3138 \\ 2x+160+z=3138\text{ Eq. (4)} \\ 10x+20(x+160)+30z=59060 \\ 10x+20x+3200+30z=59060 \\ 30x+3200+30z=59060\text{ Eq. (5)} \end{gathered}`

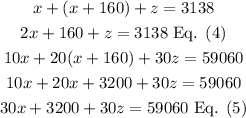
Now you have two new equations 4 and 5. Solve for z in Eq. (4):

`\begin{gathered} 2x+160+z=3138 \\ z=3138-160-2x \\ z=2978-2x\text{ Eq. (6)} \end{gathered}`

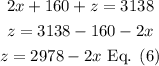
Replace this value into Eq 5 and solve for x:

`\begin{gathered} 30x+3200+30(2978-2x)=59060 \\ 30x+3200+89340-60x=59060 \\ 92540-30x=59060 \\ 92540-59060=30x \\ 33480=30x \\ x=(33480)/(30) \\ x=1116 \end{gathered}`

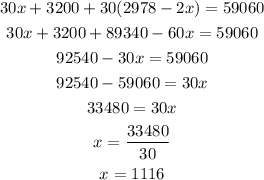
Now, replace the x-value into Eq 6 and find z:

`\begin{gathered} z=2978-2\cdot1116 \\ z=746 \end{gathered}`

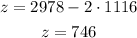
And replace x-value into Eq. (2) to find y:

`\begin{gathered} y=1116+160 \\ y=1276 \end{gathered}`

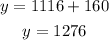
Answer: Thus, 1116 $10 tickets were sold.

1276 $20 tickets were sold.

And 746 VIP seats ($30) were sold.