Question

Objects with masses of 154 kg and 227 kgare separated by 0.454 m. A 76.5 kg mass is placed midway between them 0.454 mFind the magnitude of the net gravitationalforce exerted by the two larger masses on the76.5 kg mass. The value of the universal gravi-tational constant is 6.672 × 10-11 N - m?/kg?

Answer 1

7.23x10^-6 N

Explanation:

Given:

m1 = 154 kg

m2 = 227 kg

m3 = 76.5 kg

d12 = 0.454 m

d13 = x m

d23 = (0.454 - x) m

F31 = Force on m3 due to m1

F32 = Force on m3 due to m2

The situation of the problem can be seen in the following image:

We calculate the forces mentioned above, just like this:

`\begin{gathered} F_(31)=(G\cdot m_1\cdot m_3)/(x^2) \\ F_(32)=(G\cdot m_1\cdot m_2)/((0.454-x)^2) \end{gathered}`

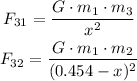
Now, can m3 in midway:

`\begin{gathered} x=(0.454)/(2) \\ x=0.227 \end{gathered}`

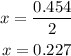
Replacing:

`\begin{gathered} F_(31)=\frac{6.672*10^(-11)^{}\cdot154_{}\cdot76.5_{}}{(0.227)^2}=1.525\cdot10^(-5)\text{ N} \\ F_(32)=\frac{6.672*10^(-11)\cdot227\cdot76.5_{}}{(0.227)^2}=2.248\cdot10^(-5)\text{ N} \\ F_(32)>F_(31) \end{gathered}`

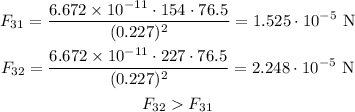
Since the force F31 is less than the force F32, we calculate the net force as follows:

`\begin{gathered} F_{\text{net}}=F_(32)-F_(31) \\ F_{\text{net}}=2.248\cdot10^(-5)-1.525\cdot10^(-5) \\ F_{\text{net}}=0.723\cdot10^(-5)=7.23\cdot10^(-6)\text{ N} \end{gathered}`

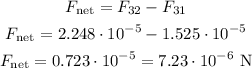
The magnitude of the force of the net gravitational force is 7.23x10^-6 N