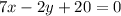We know that two lines are parallel if and only if their slopes are equal. For this reason, we need to find the slope of line given by the equation 7x-2y-5=0 in order to get the slope of the equation we are looking for; to do this we solve the equation for y:
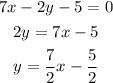
Now, this equation is written in slope-intercept form:

Comparing it with the equation we found we conclude that the slope is 7/2 and hence the equation we are looking for will also have this slope.
Now that we know this, we have to remember that the equation of a line that passes through the point (x1,y1) and has slope m is given by:

Plugging the slope we found and the point given we have:

Therefore, the equation of the line we are looking for in slope intercept form is:
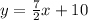
To write in general form we write it in the form Ax+By+C=0:
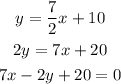
Therefore, the equation of the line in general form is: