Since the table shows points with linear behavior, we can find the rate of change (slope) by taking a pair of points. For instance, if we choose the points
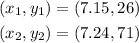
the rate of change is given by
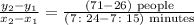
which gives
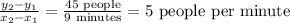
Therefore, the rate of change is: 5 people per minute.