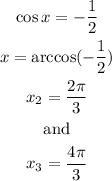Question

Solve the equation 2 cos x - sec x= 1 on the interval [0, 21)

Answer 1

The trigonometric functions cosine and secant are related by the next formula:

`\sec x=(1)/(\cos x)`

Substituting this relation into the equation, we get:

`\begin{gathered} 2\cos x-\sec x=1 \\ 2\cos x-(1)/(\cos x)=1 \end{gathered}`

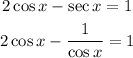
Multiplying by cos(x) at both sides of the equation:

`\begin{gathered} \cos x\cdot(2\cos x-(1)/(\cos x))=\cos x\cdot1 \\ 2\cos ^2x-1=\cos x \\ 2\cos ^2x-1-\cos x=\cos x-\cos x \\ 2\cos ^2x-\cos x-1=0 \end{gathered}`

Substituting with y = cos(x), we get:

`2y^2-y-1=0`

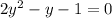
Using the quadratic formula with the coefficients a = 2, b = -1, and c = -1, the solution to this equation is:

`\begin{gathered} y_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ y_(1,2)=\frac{1\pm\sqrt[]{(-1)^2-4\cdot2\cdot(-1)}}{2\cdot2} \\ y_(1,2)=\frac{1\pm\sqrt[]{9}}{4} \\ y_1=(1+3)/(4)=1 \\ y_2=(1-3)/(4)=-(1)/(2) \end{gathered}`

In terms of the x-variable, the solutions are:

`\begin{gathered} \cos x=1 \\ or \\ \cos x=-(1)/(2) \end{gathered}`

x must be in the interval [0, 2π). Taking this interval into account, the solution to the first equation is:

`\begin{gathered} \cos x=1 \\ x=\arccos (1) \\ x_1=0 \end{gathered}`

And the solutions to the second equation are:

`\begin{gathered} \cos x=-(1)/(2) \\ x=\arccos (-(1)/(2)) \\ x_2=(2\pi)/(3) \\ \text{and} \\ x_3=(4\pi)/(3) \end{gathered}`