The question is:

This means it is required to find the z-score for 0.05.
To do this, you have to refer to the Area Under Normal Distribution Table.
z-scores are given along the 1st column and 1st row.
The value 0.05 is the significance level. We have to find its corresponding confidence level. To do that, subtract from 0.5:
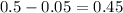
The z-score for 0.45 is the same as the z-score for 0.05.
Check this or its approximate value in the table:
You'll see for 0.4495.
This falls on 1.6 under .04
Add them together to get 1.6+0.04=1.64
The z-score is 1.64.