Question

A triangular farm is shown in the diagram below. The edges A and B are located on a bank of the river, while the farm house is located at C on the opposite bank of the river, at a safe distance from the river. The distance from point A to point B is 300 m. The angles ABC and CAB are 60° and 52°, respectively.5260A300 mB(a) Find the size of angle BCA.(b) (i) Calculate the distance from A to C(ii) Calculate the distance from B to C(iii) Find the length of the perimeter of the farm.The cost of fencing is $150 per metre.(c) Calculate the total cost of fencing the whole perimeter of the farm, rounding your answer to the nearest dollar.(d) Calculate the area of the farm, rounding your answer to the nearest square metre.(e) Calculate the shortest distance from the house to the river bank.

Answer 1

Given:

a triangular farm is shown as below

Find:

we have to find the answer from part (a) to part (e) as asked in the question.

Step-by-step explanation:

(a) we know, in a triangle, the sum of all the angle is 180° .

Therefore,

∠C + 52° + 60° = 180°

∠C + 112° = 180°

∠C = 180° - 112°

∠C = 68°

Therefore, the size of angle BCA is 68°.

.......................................................................................................................

(b) (i) Let AC = b meter and BC = a meter

Therefore by law of sines, we get

`\begin{gathered} (AC)/(sin60^o)=(AB)/(sin68^o) \\ (b)/((√(3))/(2))=(300)/(0.9272) \\ b=(300)/(0.9272)*(√(3))/(2) \\ b=280.21\text{ }m \end{gathered}`

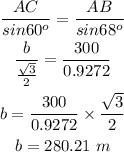
Therefore, distance from A to C is 280.21 m.

.......................................................................................................................................

(b)(ii)

Now, again by laws of sines

`\begin{gathered} (BC)/(sin52^o)=(300)/(sin68^o) \\ (a)/(0.7880)=(300)/(0.9272) \\ a=(300)/(0.9272)*0.7880 \\ a=254.96\text{ }m \end{gathered}`

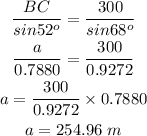
Therefore, the distance from B to C is 254.96 m.

.......................................................................................................................

(b)(iii)

The length of perimeter of farm is = 300 + 280.21 + 254.96 = 835.17 m

......................................................................................................................................

(c) The cost of fencing is $150 per meter.

The total cost of fencing the whole perimeter of the farm is

= 150 × 835.17 = $125275 (by rounded to the nearest dollar)

...................................................................................................................................

(d)

Draw a line CD perpendicular to AB as shown below

Now, in triangle ACD, we have

`\begin{gathered} sin52^=(CD)/(AC) \\ 0.7880=(CD)/(280.21) \\ CD=0.7880*280.21 \\ CD=221.59\text{ }m \end{gathered}`

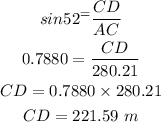
Now the area of triangular farm is

`\begin{gathered} Area=(1)/(2)* AB* CD \\ Area=(1)/(2)*300*221.59 \\ Area=33238.5\text{ }m^2 \end{gathered}`

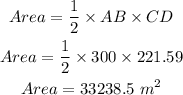
Therefore, Area of the triangular farm is 33238 square metre.

...................................................................................................................

(e)

we know the shortest distance between two points is straight line.

Therefore, the shortest distance between House C and river bank AB is CD = 221.59 metre.

.....................................................................................................................