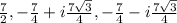SOLUTION
Given the question, the following are the solution steps to answer the question.
STEP 1: Write the given equation.
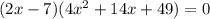
STEP 2: Find the solutions to the statement
First splitting the equation into two, we have:
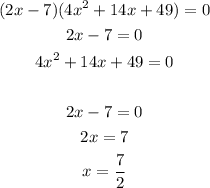
STEP 3: Find the solution to the second equation

By substitution,
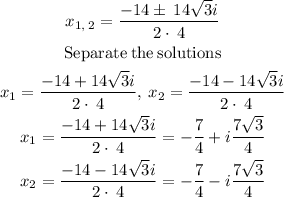
Hence, the solutions to the statement are: