We know that the population is modeled by a linear equation, this means that the model has the form:

where m is the slope of the linear model and b is the intercept of the model (the initial population). Since the population in week zero is 8, this means that b=8 and we have:
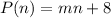
To determine the value of m we use the fact that after 6 weeks (n=6) the population is 26, then:
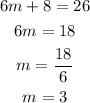
hence the slope is 6 (this means that each week there are three more beetles).
Therefore, the model of the population is given by:
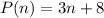
To determine after how many weeks the population is 74 we equate our expression to 74 and solve for n:
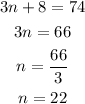
Therefore, it takes 22 weeks to have 74 beetles.