Answer:
20√2 ft
Explanation:
Given the perimeter of a square = 80 ft.
We want to find the length of the square's diagonal.
For a square of side length, s, the perimeter is calculated using the formula:
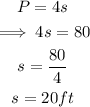
The square has a side length of 20 ft.
Next, we find the length of the diagonal.
The diagonal of a square divides it into two equal right triangles as seen in the diagram above.
Using the Pythagorean theorem, we find the value of x.
![\begin{gathered} \text{Hypotenuse}^2=\text{Altitude}^2+\text{Base}^2 \\ x^2=20^2+20^2 \\ x^2=400+400 \\ x^2=800 \\ x=\sqrt[]{800}=\sqrt[]{400*2} \\ x=20\sqrt[]{2}\text{ ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ts1qfuroejvnwugz7f5c4iiwao363axwke.png)
The length of the diagonal is 20√2 ft.