Question

Find a 95% confidence interval for the proportion of the population of voters who prefer Candidate A if there are 200 out of 500 people in our sample who prefer Candidate A.

Answer 1

`\text{ C.I = (0.3321 , 0.4679)}`

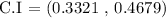
Step-by-step explanation:

Here, we want to construct a 95% confidence interval

We proceed as follows:

The number of positives x is 200

The sample size which is the total number of respondents is 500

Now, we proceed to get the sample proportion. This is the number of positives divided by the sample size

Mathematically, we have this as:

`P_(hat)=(200)/(500)=\text{ }^{}_{}0.4`

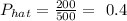
The critical level of significance α = 0.05 and z for this value is 1.96

The 95% confidence interval is thus:

`C.I\text{ = }(P_(hat)\text{ }\pm\text{ z}\sqrt[]{(P_(hat)(1-P_(hat)))/(n)}\text{ )}`

Substituting the values, we have it that:

`\begin{gathered} CI\text{ = (0.4 - 1.96}\sqrt[]{(0.4(0.6))/(200)\text{ ,}}\text{ 0.4 + 1.96}\sqrt[]{(0.4(0.6))/(200)\text{ )}} \\ \\ CI\text{ = (0.3321 , 0.4679)} \end{gathered}`