Question

Plato classes Which are features of function g if g(x)=4log(x)+4 ?

Answer 1

ANSWERS

• x-intercept of (0.1, 0)

,

• vertical asymptote of x = 0

,

• range of (-∞, ∞)

Step-by-step explanation

The given function is,

`g(x)=4\log x+4`

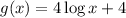
• One of the main characteristics of the logarithmic function is that the logarithm is not defined for 0 - in other words, x cannot be 0. Therefore, it has a vertical asymptote at the value of x where the argument of the logarithm is 0. In this case, the vertical asymptote is at x = 0.

• As explained before, the argument of the logarithm cannot be zero, which means that for this function there is no y-intercept.

• On the other hand, there is an x-intercept - which happens when the value of the function is 0, so, to find the x-coordinate of the x-intercept we have to solve:

`4\log x+4=0`

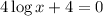
Subtract 4 from both sides,

`\begin{gathered} 4\log x+4-4=0-4 \\ 4\log x=-4 \end{gathered}`

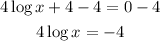
Divide both sides by 4,

`\begin{gathered} (4\log x)/(4)=(-4)/(4) \\ \\ \log x=-1 \end{gathered}`

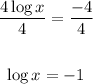
And raise the base of the logarithm - which is 10, to each side of the equation,

`\begin{gathered} 10^(\log x)=10^(-1) \\ \\ x=(1)/(10)=0.1 \end{gathered}`

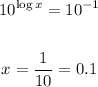
So, the x-intercept is (0.1, 0)

• For the domain, since the argument of the logarithm cannot be 0 or negative, the domain of this function is x > 0, which in interval notation is (0, ∞) and not (4, ∞) as suggested in the options.

• Finally, the range of the function is the set of all the values the function can take in the domain. In this case, in the defined domain, the function can take any value, so the range is all real values.

Hence, the correct features of function g are:

• x-intercept of (0.1, 0)

,

• vertical asymptote of x = 0

,

• range of (-∞, ∞)