Question

2 (-2, 0); y = -2x - 4y = x+4What are the steps

Answer 1

To solve the system given

`\begin{gathered} y=-2x-4 \\ y=x+4 \end{gathered}`

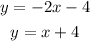
we substitute the value of y from the first equation to the second. This gives

`-2x-4=x+4`

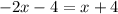
adding 2x to both sides gives

`-2x-4+2x=x+4+2x`
`-4=3x+4`

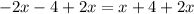
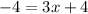
subtracting 4 from both sides gives

`-8=3x`

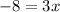
Finally, dividing both sides by 3 gives

`\boxed{x=-(8)/(3)\text{.}}`

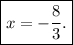
With the value of x in hand, we substitute it into y = x +4 to get

`y=x+4`
`y=-(8)/(3)+4`
`\boxed{y=(4)/(3)}`

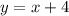
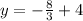
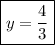
Hence, the solution to the system is

`(-(8)/(3),(4)/(3))`

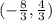
which is our answer!